NEW IN STORYLINE 360: New Triggers Panel and Workflow
Oct 29, 2019
Storyline 360 just got even better. Now you can more easily manage your triggers and work faster with the new triggers panel and workflow.
You can quickly make edits to triggers directly in the trigger panel with easy-to-use drop-down lists. You can collapse triggers and group them by event type, so they’re easier to find and make changes to. You can also click and drag to change the order of triggers. Plus, you can disable individual triggers for faster troubleshooting.
You can turn the new workflow on and off at any time in your Storyline 360 options. We think you’re going to love it!
Check out this video to see the new triggers panel and workflow in action:
76 Replies
AT LAST! This is a huge upgrade to everyone's workflow.
Grouping and batch editing is...ahem...IUUUGE !!!
You guys took our feedback and really listened this time. Color me impressed. Congrats & Kudos to the team for the implementation.
Nice work, Articulate. The color highlighting really does help.
Loving everything about this update!
Great update. I love the way we can work with triggers now. It has already speeeeeded up my work. Thanks guys!
FYI you'll need to update in the Articulate 360 panel. A direct download still gives you the old version.
Having used this for what seems like a year, it is a huge upgrade, if you want to change and object based on the states of other objects, highlight those objects before you start the trigger and it will pull them into the trigger. It is now really simple to group timeline start triggers swap the to an object and the copy to another slide. Real productivity gains, Articulate did some amazing work here.
This is an amazing upgrade. Triggers are at the core of the development process. Like Phil, I have also used this as a test user for a while, and it has cut production time in half.
Will this be applied to Storyline 3 at all? If it will be what is the timeline on this?
Awesome work, such an improvement.
So glad it's finally here!
As a person who uses Storyline often and utilizes advanced features often, this update is fine. I especially love the collapsing of triggers for an object.
As a person who just had to help all of the other Storyline users at my work who are not very technology savvy, this update was a headache for them. The color change to the triggers brought some question to whether or not color blind users would have issues identifying the modifiable parts of the trigger in the list.
One of my users opened a trigger to the new Trigger Wizard screen and seemed very overwhelmed. The Trigger Wizard appearance changed from easily identifiable dropdown boxes to small words or sometimes characters (like > or =) that have to be clicked on in exactly the right spot on the screen to edit. Users are familiar with the functionality of a dropdown box because it's all over the internet, but the move toward minimalism has left my novice Storyline users with feeling like they aren't quite sure what to do in the new wizard.
I want to reiterate, I will have no trouble getting used to these changes, but I do worry that this change might make things harder on the user experience end for those who aren't Storyline super users like a lot of others are.
I like the new Trigger manipulation, but I can't seem to find the checkbox there used to be for "Ignore Case" when using Text entry fields. I haven't been using Storyline but a few weeks, so maybe I'm mistaken, but I thought it was in the conditions for a Text variable I was able to set the Ignore Case option.
Am I just mis-remembering, or has it been moved somewhere?
I love this update. The new trigger panel is my favourite feature (EVER!) and makes workflow much easier/quicker when dealing with triggers.
This post was removed by the author
This is great, but there is a bug where trigger selection loses focus when deleting the first trigger on an object. One has to reselect an object to be able to delete all triggers on that object.
Liking the look of the new trigger workflow. Good work Articulate.
love this!! thank you Articulate team!!
I can't seem to find this either Robert. Can anyone shed any light?
Hi David and Robert,
You can find the ignore case trigger in the dropdown when you select the equal sign as in the attached picture. Hope that helps!
Thanks! I knew it had to be there somewhere. If I weren't so new with Storyline perhaps I would have found it on my own.
Thanks again!
Thanks Annie, that's really helpful.
All that work and no if/else?? I am honestly extremely disappointed. What the heck is the problem? Without an else clause EVERY damned thing I try and do is littered with triggers that are all over the place. Even worse, I get to make two buttons now that show and hide each other in order to do something as simple as a button toggles a boolean.
Apparently it was possible in Storyline 3... but the drop down no longer shows any Operator options.
I am facepalming with my fist right now. Crossing fingers and hope I just haven't opened the right panel somehow, at which point I will complain it isn't in the trigger wizard window...
Love love love this. I have been describing the need for this with our team for months now. Now I can be quiet, it is here! Unfortunately the web object changes are stopping us from updating. We are still trying to solve it from our end in the meantime. There is only one of our typically web objects that is currently working. Survey monkey gets enlarged and all the rest of our web objects do too.
I turned off the "new hotness" wizard and found the Operator I was looking for...
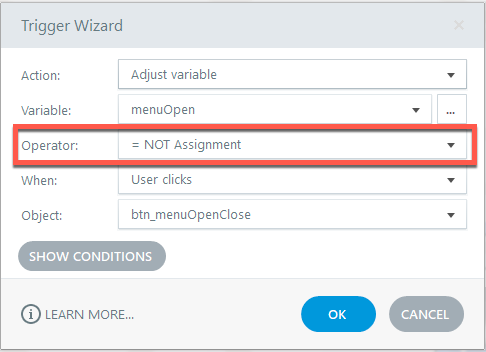
I can't fathom why the capability has gone backwards in order to support the new trigger wizard.
But my rate * my time tells me you guys owe me a refund...
Joking... but still a little miffed.
Rusty, toggle is (and always has been) possible with one trigger
No if/else, the productivity gains you will get will from this panel and wizard are real.
This discussion is closed. You can start a new discussion or contact Articulate Support.